Exponential Functions Integration Example 5A

This is a continuation of example 5.  It shows how you would do the previous Exponential Integration problem using 'u' substitution. 

Post any questions in the comments.

 

Exponential Functions - Integration Example 5

I realize this is a challenging example. If there are any questions, please leave a comment, I will answer them.

I solved this problem using a given formula for the integration of exponential functions.

Although this method works for most all exponential integration problems, I will still upload another post showing how you would do this problem using a 'u' substitution method. 

This method is a lot faster than 'u' substitution, and it would benefit you to go for it in an exam type situation.
 

Exponential Functions Example 4

Integrating Exponential Functions
Post any questions in the comments

Exponential Functions- Integration Example 3

Integrating Exponential Functions

 Post any questions in the comments
Got a Cute Pet Pic? Free Entry! New $1000 Winner Every Month

Exponential Functions - Integration Example 2

Post any questions in the comments.  

Exponential Functions - Derivative Ex3

I will not post any more exponential derivative examples unless requested. They are quite trivial.
Please post any questions in the comments
 

Exponential Functions - Derivative Example 2

 

Exponential Functions - Derivative Example 1

Finding the derivative of exponential functions.
Post any questions in the comments.

 

The Natural Logarithm - Logarithmic Differentiation Example 6

Calculus
How do you do logarithmic differentiation?
Below is example 6.
Post any questions in the comments.
http://simplecalc.blogspot.com

 

The Natural Logarithm- Logarithmic Differentiation Example 5

Post any questions in the comments

The Natural Logarithm - Logarithmic Differentiation Example 4

Sometimes the trickiest part of Logarithmic Differentiation is dealing with the f(x) symbol. Remember the rules apply to ln(f(x)) the same as they do to ln(x).
Below is a step by step example of how to do a simple Logarithmic Differentiation. More complicated examples will be uploaded shortly.

Post any questions in the comments and I will try to answer as quickly as possible.

Log Ex4

The Natural Logarithm - Integration Example 3

 

The Natural Logarithm - Integrals involving the natural logarithm Example 2

If you have not seen example 1 please refer to it before proceeding.
Integrating the Natural Logarithm often involves substituting and rearranging the function in order to get it to resemble the form 1/x 

Usually 'u' substitution is used to do so.

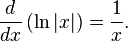http://en.wikipedia.org/wiki/Natural_logarithm#The_natural_logarithm_in_integration

http://en.wikipedia.org/wiki/Natural_logarithm#The_natural_logarithm_in_integration

Below are two separate problems that deal with integration of the logarithmic function.

Don't forget to add the constant at the end of every indefinite integral.
Double Click on Image to make it larger.

The Natural Logarithm - and the Calculus of its functions.

Below is an example problem involving the Natural Logarithm.  It is a common problem, that uses elementary calculus principles to find the derivative of the Natural Logarithm.  The one below requires use of the quotient rule.  I will post more examples in the future involving integrals.

Calculus- Find the Work Required To Remove Water From a Container Example 2

If you have not looked at example 1 please do so before continuing.

In this example a spherical container of radius 10 that rests on the ground, is filled with water.
Compute the work required to remove all the water through the top of the spherical container. 

Using the same equation as in example 1, we solve for x^2 using the familiar Pythagorean Theorum, and then simply substitute values to find the equation of for integration.

Because the water is exiting from the top the distance it must travel is 20-y.   The reason it is 20-y and not just 20, is because each layer is not being moved a distance of 20. In other words, the distance gets shorter for each successive layer.

Double Click on Image To Zoom.
Post any questions in the comments. 

Calculus- Finding the Work Required to Fill a Tank Example 1

A common level 2 calculus question is to ask for the work required to move a liquid a certain distance, or into a tank of some common geometric shape. Sometimes the tank is spherical, conical, or cylindrical.

In the problem below we explore a question involving a spherical tank.
The center of the tank is elevated to a height of 150 meters from the ground.  The radius of the tank is 25 meters.
We are asked to compute the work done by filling the tank up to a level of 125 meters with homogeneous water. 

Note:
-Remember that work depends on initial and final state of the water or liquid.
-The weight of each 'dy' layer of water is different and the distance each 'dy' layer must be moved is also different.
-Our strategy is to compute the work required to move one tiny layer, then use our knowledge of integration to sum all the layers together.
-The problem assumes that the liquid being moved is homogeneous, this means that it is of uniform density throughout. 
-Be certain of the interval over which you are integrating.  Sometimes they ask to pump the water out of the tank through the top rather than into the tank through the bottom.
-In this problem we need only integrate from 100 meters to 125 meters since that is the height the water must be pumped to. 

Calculus - Finding the Arc Length of a Curve

In general Arc Length integral can be very difficult to compute by hand.  In most calculus courses the professors only ask you to set up the integral. 

Below the equation for Arc Length is given as well as an example problem.  This problem requires 'u' substitution to be solved completely.  The answer is left in unsimplified terms. 

Double Click on Image to make larger.
Post any questions in the comments section.

Calculus- Finding Volume By Cylindrical Shells

Sometimes using the methods of washers or discs creates an unpleasant integral.
This is why the method of Cylindrical Shells is used.

To help visualize this method, think of a solid can in the shape of a cylinder.

Now imagine unraveling the paper label that covers the outer surface of the can. Although it is small, it is still a portion of the total volume.

If we keep unraveling this can in thin strips such as the paper label, and we then sum all of the strips up we will have the total volume.  A visual representation of this is shown in figure 1. 

if you unravel each strip and flatten in out, it would have a height, length (same as circumference), and width (represented as 'dx').

In figure 2 the equation for finding the volume using Cylindrical Shells is shown.

Question (Figure 3): Find the volume of the region bounded by y=  x²  , x= -2 and x = 2
The radius is along the x-axis of length 'x'
The height extends from the x-axis up to the curve.   
The thickness of each sheet is represented by 'dx'
Input all of these parameters into the equation.

Post any questions in the comments.
Double-click on image to make it bigger.

Using the Method of Washers to Find Volume

Calculus - Use Method of Washers to Find Volume.

 

DOUBLE CLICK ON IMAGE. It's a landscape width. 

Finding Volume Using Method of Washers Example 3

This problem involves integrating a region revolved around a line. 
The integration is in the y direction.
Identify the outer radius and the inner radius. 
The region should look like a cylinder of height 3, with a conical shape drilled out of it. 

note: if you cannot see image properly double click on it. 
leave a comment if you have any questions.

Calculus of Disks, Washers, Slicing -- Example 2 Using Washers

This method is fairly simple, and involves identifying an inner and outer radius.
It is very similar to the method of disks.
I will upload more involved examples, but for now these are the basics.

 

If you have any questions please post it in the comment box.  If it is substantial I'll make another post about it, if not I will just reply as a comment. 

Note: If you double click on the image it should open in another tab, there you can view it at a larger size.  

 

Volume Using the Method of Disks (Discs), Slicing, and Washers Example 1

My personal notes on using the method of disks. 
Remember, Calculus is all about the infinitesimal.  In this example I graph the region and split it up into an infinite number of disks and sum them all together. 

The idea of finding volumes by slicing/disks/washers is one explored in great detail in most Calculus 2 courses. You have to visualize the graph not as a whole, but as many smaller parts added together. 

Area Between The Curves - Using the Definite Integral

I will skip the preliminaries of describing the definite integral.
You can use the definite integral to find the area between two curves.
Simply draw the graphs and then determine the region over which you are integrating.

The hardest part is to draw the graphs and identify the region in question. Once you have done that it just becomes a matter of crunching numbers and integrating.

note: if image is too small, double-click on it and it should open in a separate page where you can zoom.